AIを賢く強力に進化させるための強化学習の種類と概要を学ぶ • AItomo.blog

はじめに
強化学習とは
1. 強化学習の基本的な考え方
  1. 強化学習における報酬とは
AIに強化学習することで何が変わるのか
主な強化学習のアルゴリズムの種類
詳しいアルゴリズム：Q学習 (Q-Learning)
詳しいアルゴリズム：DQN (Deep Q Network)
詳しいアルゴリズム：DDQN (Double DQN)
詳しいアルゴリズム：A3C (Asynchronous Advantage Actor-Critic)
詳しいアルゴリズム：Rainbow
詳しいアルゴリズム：Prioritized Experience Replay:
1. TD誤差について
詳しいアルゴリズム：Dueling Networks
詳しいアルゴリズム：Learning from Multi-step Bootstrap Targets
詳しいアルゴリズム：Distributional DQN
詳しいアルゴリズム：Noisy DQN
他のアルゴリズム：
おわりに

はじめに

AIを賢く強力に進化させるための強化学習について強化学習とは、種類、概要を説明していきます。そんなものがあるのかと知ることでAIの知識を取り入れ学びたい方のために執筆しました。少し難しい内容になるのでさらっと読むもいいしじっくり読むのもいいと思います。

強化学習とは

強化学習は、機械学習の一種で、システム（エージェントと呼ばれます）が試行錯誤しながら、最適なシステム制御を実現する手法です。

強化学習の基本的な考え方

エージェントはある環境内で行動します。
その行動によって環境は変化し、エージェントはその結果を観測します。
行動の結果としてエージェントは報酬（またはペナルティ）を受け取ります。
エージェントの目標は、時間を通じて得られる報酬の合計を最大化することです。
このプロセスは試行錯誤を通じて行われ、エージェントは最適な行動を学びます。この「最適な行動」は、特定の状況下で最高の結果をもたらす行動のことを指します。

強化学習は、自動運転車の制御、ゲームプレイ（チェスや囲碁など）、ロボットの動作学習など、多くの応用分野で使用されています。また、強化学習の一部として深層強化学習（Deep Reinforcement Learning）があり、これはディープラーニングを強化学習に適用したもので、より複雑な問題を解決するのに有用です。強化学習は非常に活発な研究分野で、新しいアルゴリズムや改良が常に提案されています。

強化学習における報酬とは

AI学習、特に強化学習における「報酬」は、エージェント（AI）が行動を選択することで環境から得られるフィードバックのことを指します。報酬は、エージェントがどの程度良い行動を取ったかを評価する基準となります。

具体的には、エージェントがある行動を取った結果、その行動が目標達成に対して良い結果をもたらした場合、エージェントは正の報酬を得ます。逆に、その行動が目標達成に対して悪い結果をもたらした場合、エージェントは負の報酬を得るか、または報酬を得られないことがあります。

例えば、バスケットボールのゲームをAIに学習させる場合、パスが成功するたびに1ポイント、得点が入ると50ポイントといった報酬を設定することができます2。このように、報酬はエージェントがどの行動を選択すべきかを学習するための重要な指標となります。

また、報酬はエージェントが最適な行動を学習するための「教師」の役割を果たします。エージェントは、報酬を最大化するような行動を学習することで、目標達成に向けた最適な行動を見つけ出します。

報酬の設定は、AIの学習結果に大きな影響を与えます。適切な報酬を設定することで、AIは効率的に学習を進め、より良い性能を発揮することができます。しかし、報酬の設定は難易度が高く、AIの学習結果を最適化するためには、適切な報酬設計が必要となります。

エージェント→行動→報酬→評価のような順序でトレーニングします。

AIに強化学習することで何が変わるのか

強化学習をAIに適用することで、AIは自己学習を通じて最適な行動を学び、複雑なタスクを自己学習でこなすことができるようになります。

自律的な学習：

AIは試行錯誤を繰り返しながら、最適な行動をするように学習します。これにより、AIは人間の介入なしに自己学習と改善を行うことができます

複雑な問題の解決：

強化学習は、ゲームの最適化やロボットのタスク自動化など、複雑な問題を解決するのに適しています。例えば、囲碁やチェスなどのゲームでは、AIが人間のチャンピオンに勝つことが可能になりました。

自動運転の実現：

自動運転の分野でも、強化学習が使われています。AIは道路の状況を理解し、最適な運転行動を学習することで、自動運転をより安全にすることが可能になります。

最適な行動の探索：

強化学習では、AIは報酬を最大化する行動を探索します。これにより、AIは最適な行動を自己学習し、その行動を改善していくことが可能になります。

これらの変化は、AIがより自律的になり、人間の介入を必要としない学習と改善を可能にします。これにより、AIはより複雑なタスクを効率的にこなすことができ、その結果として、AIの応用範囲が大幅に広がります。

主な強化学習のアルゴリズムの種類

Q学習 (Q-Learning)

これは、エージェントが最適な行動を選択するための価値関数を学習する方法です。エージェントは、各行動が将来の報酬を最大化する確率を学習します。

DQN (Deep Q Network)

これは、Q学習を深層学習と組み合わせたものです。ニューラルネットワークを使用して価値関数を近似し、より複雑な問題を解決することができます。

DDQN (Double DQN)

これは、DQNの改良版で、過大評価問題を解決するために開発されました。2つのQネットワークを使用して、行動の選択と評価を分離します。

A3C (Asynchronous Advantage Actor-Critic)

これは、複数のエージェントが非同期に学習を行う方法です。これにより、学習速度が向上し、局所最適解からの脱出が容易になります。

Rainbow

これは、複数の強化学習の技術を組み合わせたものです。DQN、DDQN、Prioritized Experience Replayなどの技術を組み合わせて、性能を向上させています。

詳しいアルゴリズム：Q学習 (Q-Learning)

Q学習は強化学習の一種で、エージェントが未知の環境を探索しながら最適な行動を学習するためのアルゴリズムです。
Q学習では、エージェントが行動価値関数（Q関数）を学習し、この関数を使用して最適な行動を選択します。Qとは、Qualityの略であり、行動の質を示す値として利用されます。

Q学習のアルゴリズムは以下のような簡単な式で表現可能です：

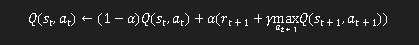
1.Q(st,at)はある時点tにおける状態s、行動aによるQ値です。
2.αはQ学習の学習率を示すもので0～1の値を取り、これによって新たなQ値を更新します。
3.rは報酬を意味し、rt+1は次の状態での報酬がどうなっているのかを意味します。
4.γは割引率と呼ばれ0～1の値を取り、0に近くなるほどその場の報酬を重視し、逆に1に近づくと将来の報酬を重視するようになります。
5.maxat+1Q(st+1,at+1)とは次に取りうる状態と行動の内、最も大きなQ値を選んでいます。

Q学習は、エージェントが未知の環境を探索しながら最適な行動を学び、その結果として得られる報酬を最大化することを目指す強化学習の一種です。

以下に、Q学習の具体的な例をいくつか紹介します：

ゲームプレイ：GoogleのAlphaGoは、囲碁の世界チャンピオンに勝利した例が有名です。AlphaGoはQ学習を用いて、数多くの試合を通じて最適な手を学びました。

迷路の解決：Q学習は、エージェントが迷路を解く問題にも適用されます。エージェントは迷路の各位置（状態）での最適な行動（上下左右に移動する）を学び、ゴールに到達する最短の経路を見つけます。

自動運転：自動運転車の制御にもQ学習が使われています。エージェント（自動運転システム）は、道路の状況や他の車の動きを考慮して最適な運転行動（加速、減速、旋回など）を学びます。

資源管理：強化学習はエネルギー消費を最小化しながら生産効率を最大化するような資源配分を学ぶのに使われます。

詳しいアルゴリズム：DQN (Deep Q Network)

DQN（Deep Q-Network）は、Q学習とディープラーニングを組み合わせた強化学習の手法です。

Q学習では、エージェントがある状態で取った行動の価値を、Qテーブルと呼ばれるテーブルで管理し、行動する毎にQ値を更新していきます。しかし、Qテーブルだけでは、連続的な「状態」、例えばロボットアームの動きのようななめらかなものを表現しようとすると、Qテーブルが膨大な量となり、現実的に計算ができなくなるデメリットがあります。

DQNでは、この問題を解決するために、Q値そのものを推定するのにニューラルネットワークを使います。具体的には、ある状態”sₜ”を入力し、行動”a”が出力層のノードとなるようなニューラルネットワークを使用して”Q (sₜ,aₜ)”の値を計算します。これにより、連続的な行動にも対応できるようになっています。

DQNの学習プロセスは以下のようになります：

1.Q-networkに状態を入力し、Q (sₜ,aₜ;)を求める
2.ε-greedy法に従い、行動をして報酬を求め、sₜ,aₜ,Rₜ,sₜ₊₁,Q (sₜ,aₜ)を保存
3.誤差関数を求め、Q-networkの重みを更新
4.設定した試行ステップごとにTarget-Networkの重みを更新
①溜めている過去sₜ,aₜ,Rₜ,sₜ₊₁,Q (sₜ,aₜ)のから任意の個数を取得
②そのデータを利用して、設定したミニバッチ数でTarget-networkの重みの学習を行なう (Experience Replay)
③求められたTarget-networkの重みをQ-networkと同期
5.更新された重みが適用されたQ-networkで、①から③を繰り返す

詳しいアルゴリズム：DDQN (Double DQN)

DDQN（Double Deep Q-Network）は、DQN（Deep Q-Network）の改良版で、Q学習の過大評価問題を解決するために開発されました。

DQNでは、行動を決定するときに使うネットワークと、その行動を評価するときに使うネットワークが同じであることが問題でした。つまり、自分の行動を自分で評価しているため、過大評価・過小評価になってしまうということです。

これを解決するために、DDQNでは自分の行った行動を「第三者」に評価してもらうというのが基本的な考え方です。具体的には、行動決定用ネットワークと価値計算用ネットワークの2つを定義し、行動決定用ネットワークによる行動決定と価値計算用ネットワークによる行動評価を分けることで、過大評価を抑制します。

DQNとDDQNの主な違いは、行動の評価方法にあります。DQNでは、行動の評価に同じネットワークを使用しますが、DDQNでは行動の評価には別のネットワーク（価値計算用ネットワーク）を使用します。これにより、自分の行動を自分で評価するという問題を解決し、より正確な行動価値の推定が可能になります。

DDQNの学習プロセスは以下のようになります：

1.行動決定用ネットワークによる行動決定
2.実際に行動を行ってみる
3.行動決定用ネットワークの重みを価値計算用ネットワークにコピー
4.学習可能なくらい経験がたまったら学習を行う
5.ターゲットデータと教師用データで行動決定用ネットワークを更新

詳しいアルゴリズム：A3C (Asynchronous Advantage Actor-Critic)

A3C（Asynchronous Advantage Actor-Critic）は、強化学習のアルゴリズムの一種で、非同期の学習を用いて強化学習エージェントを訓練する手法です。

A3Cの名称は、「Asynchronous」、「Advantage」、「Actor」、「Critic」の4つの要素から成り立っています：

「Asynchronous」は「非同期」という意味で、複数のエージェントによる非同期な並列学習を行うことを指します。
「Advantage」は、複数ステップ先を考慮して更新することを指しています。
「Actor」および「Critic」は、Actor-Critic手法と関わっています。Actor-Critic手法は強化学習の学習のアプローチの１つで、行動を決めるActor（行動器）を直接改善しながら、方策を評価するCritic（評価器）を同時に学習させます。
A3Cの特徴は、複数のエージェントが同じ環境で非同期に学習することです。各エージェントが並列に、自律的にrollout (ゲームプレイ) を実行し、そこで計算した勾配の情報に基づいて、「それぞれのタイミング」で共有ネットワーク (global network) を更新します。そして、各エージェントはそれぞれ定期的に自分のネットワーク (local network) の重みを共有ネットワークの重みと同期します。

A3Cの利点は、ネットワーク全体と重みを共有しつつ、並列分散的に学習しているため、学習が高速化できることと、学習を安定化できることです。経験の自己相関による学習の不安定性は強化学習分野の長年の課題でしたが、A3Cは、経験の自己相関を低減するために、エージェントを並列化する工夫をとっています。

一方で、A3Cの難しいところは、Pythonのプログラミング言語の特性上、非同期並列処理を行うのがやや面倒であること、また、同時並列的に学習するため、A3Cの実装はそれなりに大規模な計算リソースのある環境が必要であることです。

詳しいアルゴリズム：Rainbow

Rainbowは、強化学習のアルゴリズムの一種で、複数の強化学習の手法を組み合わせたものです。

Rainbowは、以下の7つの主要な強化学習の手法を組み合わせています：

1.DQN (Deep Q-Networks): Q学習とディープラーニングを組み合わせた手法で、行動価値関数（Q関数）をニューラルネットワークで近似します。
2.Double DQN: DQNの改良版で、Q学習の過大評価問題を解決します。
3.Prioritized Experience Replay: 経験の再生を優先度に基づいて行うことで、学習効率を向上させます。
4.Dueling Networks: 行動価値関数を状態価値関数と行動優位性関数に分解することで、学習の安定性と効率性を向上させます。
5.Learning from Multi-step Bootstrap Targets: 複数ステップ先までの報酬を考慮することで、学習の効率性を向上させます。
6.Distributional DQN: 行動価値の分布を考慮することで、学習の安定性を向上させます。
7.Noisy DQN: パラメータにノイズを加えることで、探索性能を向上させます。

これらの手法を組み合わせることで、Rainbowは強化学習のパフォーマンスを大幅に向上させることができます。Rainbowは、自動運転、ゲームプレイ（チェスや囲碁など）、ロボットの動作学習など、多くの応用分野で使用されています。また、強化学習の一部として深層強化学習（Deep Reinforcement Learning）があり、これはディープラーニングを強化学習に適用したもので、より複雑な問題を解決するのに有用です。強化学習は非常に活発な研究分野で、新しいアルゴリズムや改良が常に提案されています。

先ほど紹介のアルゴリズム以外の強化学習アルゴリズムの説明を以下にしていきます。

詳しいアルゴリズム：Prioritized Experience Replay:

Prioritized Experience Replay（優先的経験再生）は、強化学習の手法の一つで、経験を「優先度」に基づいて再生する技術のことを指します。

通常のExperience Replayでは、過去の経験（状態、行動、報酬、次の状態）をランダムに再生して学習します。しかし、Prioritized Experience Replayでは、学習における価値の高い経験を優先的に再利用することで、学習の効率性と効果性を向上させる狙いがあります。

具体的には、目標値と学習の推定値の差で定義されるTD誤差が大きいサンプルを重点的に学習に使います。つまり、TD誤差が大きいということは、その経験から学ぶべきことが多いということを意味します。

Prioritized Experience Replayは、深層強化学習の性能向上や学習効率の改善に革命をもたらしています。

TD誤差について

TD誤差（Temporal Difference Error）は、強化学習における重要な概念で、エージェントが行動する前に予想した行動の評価値と、実際に行動してみて評価したその行動の評価値との誤差のことを指します。

具体的には、TD誤差は以下のような式で表されます：

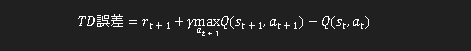
1.rt+1は次の状態での報酬を意味します。
2.γは割引率で、0～1の値を取り、0に近くなるほどその場の報酬を重視し、逆に1に近づくと将来の報酬を重視するようになります。
3.Q(st,at)はある時点tにおける状態s、行動aによるQ値です。
4.maxat+1Q(st+1,at+1)とは次に取りうる状態と行動の内、最も大きなQ値を選んでいます。

TD誤差が0になるように、行動価値関数を学習する必要があります。これは、現在のQ値と将来のQ値をα (アルファ)で指数平均しているのと同義です。γ (ガンマ)は将来のQ値に対する反映係数で、将来に対する不確定要素からくる割引率となります。

以上がTD誤差についての説明です。TD誤差は、強化学習の学習プロセスにおいて重要な役割を果たします。具体的には、TD誤差が大きい経験（つまり、予想と実際の結果が大きく異なる経験）は学習にとって価値が高いと考えられ、これを優先的に学習することで、学習の効率性と効果性を向上させることができます。この考え方は、Prioritized Experience Replayなどの強化学習の手法に取り入れられています

詳しいアルゴリズム：Dueling Networks

Dueling Networkは、強化学習のネットワーク構造を改良したモデルで、行動価値関数を状態価値関数と行動優位性関数に分解することで、学習の安定性と効率性を向上させる手法です。

Dueling Networkの最も魅力的な部分は、そのアーキテクチャにあります。伝統的なQ-learningでは、状態と行動のペアに対してQ値を推定しますが、Dueling NetworkはこのQ値の推定を2つの部分に分離して考えます。

具体的には、以下の2つの関数に分解します：

Value Function (V): 特定の状態の価値を評価するもので、行動を考慮せずに環境の状態のみに基づいて評価します。
Advantage Function (A): 各行動の価値を評価するもので、特定の状態での各行動が平均よりもどれだけ優れているか、または劣っているかを評価します。

この2つの関数を組み合わせることで、Dueling Networkは伝統的なDQNよりも効率的に学習を進めることができ、特に多数の行動を持つ問題や高度なタスクでの性能が向上することが実証されています。

Dueling Networkのアーキテクチャは、AIが環境の状態をより効果的に理解し、最適な行動を選択するための手助けをしています。具体的な応用例としては、ゲームAIの向上、ロボティクスの適用、金融市場の予測などがあります。

Dueling Networkは、DQN, DDQNなどのModel-freeなアルゴリズムと組み合わせて利用することができます。状態価値関数V (s)が行動aに寄らずに学習できることが主な利点となっています。これにより、Dueling Networkは状態や行動の価値を迅速かつ正確に推定します。結果として、学習が加速し、より早く適応的な行動ポリシーを獲得できます。このアーキテクチャは、AIが環境の状態をより効果的に理解し、最適な行動を選択するための手助けをしています

詳しいアルゴリズム：Learning from Multi-step Bootstrap Targets

Learning from Multi-step Bootstrap Targetsは、強化学習の手法の一つで、複数ステップ先までの報酬を考慮することで、学習の効率性を向上させる手法です。

具体的には、通常のQ学習では、次のステップの報酬と最適な行動価値（Q値）を用いて現在の行動価値を更新します。しかし、Learning from Multi-step Bootstrap Targetsでは、複数ステップ先までの報酬と行動価値を用いて現在の行動価値を更新します。

この手法は、未来の報酬をより直接的に考慮することで、学習の効率性を向上させることができます。具体的には、複数ステップ先の報酬を考慮することで、エージェントはより長期的な視点で最適な行動を学習することができます。

Learning from Multi-step Bootstrap Targetsは、DQNやRainbowなどの強化学習のアルゴリズムに組み込むことができます。

詳しいアルゴリズム：Distributional DQN

Distributional DQNは、強化学習のアルゴリズムの一種で、行動価値（報酬）を単一の値ではなく、確率分布として扱うことで学習のパフォーマンスを向上させる手法です。

通常のDQNでは、行動の価値（報酬）を一つの値として扱っています。しかし、Distributional DQNでは、行動の価値を確率分布として扱うことで、報酬の不確実性をより正確に捉え、学習のパフォーマンスを向上させることができます。

Distributional DQNの主な特徴は以下の通りです：

価値分布のモデリング：行動の価値を確率分布としてモデリングします。これにより、報酬の不確実性をより正確に捉えることができます。
分布ベルマンオペレータ：分布ベルマンオペレータを用いて、価値分布の更新を行います。

Distributional DQNは、強化学習の一部として深層強化学習（DeepReinforcement Learning）があり、これはディープラーニングを強化学習に適用したもので、より複雑な問題を解決するのに有用です。この手法は、Rainbowの中核を成すもので、DQNに初めて行動価値関数の分布を取り込んだモデルです。

確率分布とは

確率分布とは、「ある試行で起こり得るすべての事象の確率を出力する関数」で、離散と連続の分類があります。確率分布は、偶然性に支配される現象を記述し、可視化するための考え方です。

例えば、サイコロを振ったときの出目を考えてみましょう。サイコロの出目は1から6までの整数で、それぞれの出目が出る確率は1/6です。これを確率分布として表現すると、各出目（1, 2, 3, 4, 5, 6）が出る確率（1/6）を示すグラフになります。

一方、Distributional DQNでは、行動の価値（報酬）を確率分布として扱います。つまり、行動の価値が一つの値ではなく、確率的に複数の値を取り得ると考えます。例えば、ある行動を取ったときに得られる報酬が5ポイントである確率が0.1、10ポイントである確率が0.3、15ポイントである確率が0.6といった具体的な確率分布を考えることができます。

このように、確率分布を用いることで、行動の価値が取り得る複数の可能性を考慮に入れ、その不確実性をより正確に捉えることができます。これにより、学習のパフォーマンスが向上し、より良い結果を得ることが可能になります。

詳しいアルゴリズム：Noisy DQN

Noisy DQNは、強化学習の手法の一つで、ネットワークの重みにノイズを加えることで、広範囲の探索を実現します。

通常のDQNやその他の強化学習アルゴリズムでは、ε-greedy法がよく用いられます。これはεの確率でランダムに行動し、1-εの確率で期待値の高い行動を選択するものです。ランダムな行動によりエージェントは新しい行動を試したり、知識を更新します。しかし、これでは広い空間を探索することができません。

Noisy DQNでは、ネットワークの重みにノイズを加えることで、より広範囲の探索を可能にします。これにより、エージェントは新しい行動を試すだけでなく、未知の状態や行動に対する探索も行うことができます。これは、エージェントがより広範囲の状態と行動を学習し、より良いポリシーを見つけるのに役立ちます。

　εは何の記号？

記号εは、ギリシャ語のアルファベットで、「イプシロン」と読みます。数学や科学の記号として広く使用されています。

具体的な用途は、状況によりますが、以下のような例があります：

材料力学や建築の分野では、「歪み」を表す記号として使用されます。

電気的な分野では、「誘電率」（比誘電率）を示す記号として使用されます。

また、強化学習においては、εはε-greedy法におけるランダムな行動を選択する確率を表すパラメータとして使用されます。このε-greedy法は、エージェントがεの確率でランダムに行動し、1-εの確率で期待値の高い行動を選択する方法です。これにより、エージェントは新しい行動を試したり、知識を更新したりします。

このように、εは様々な分野で重要な役割を果たしています。